UNDERSTANDING THE MOTIVE
One of my professors at IIT Jodhpur came up with a curious question, “How do the students in a college make friends, and how does that impact their academic performance?” It seemed an interesting question to almost all the students as we all were enrolled in the course of Socio-Economic Networks. We all decided to work more on the problem statement, improvise it and form a questionnaire to collect the data. Since I had a decent command over R and had recently stumbled upon a library called igraph I decided to handle the analysis part of the project.
Problem Statement:
Network analysis is an approach to research that is uniquely suited for describing, exploring, and understanding structural and relational aspects of a relationship. Our main motive of the project was to study the friendship network in IIT Jodhpur. The whole survey questions were customized to study traits of IIT Jodhpur students.
- The main motive of the study was to find the friendship network of IIT Jodhpur.
- Carry out statistical analysis in order to find a nodal network connecting all students.
- Find clusters according to various parameters like gender, batch, region, language, academic performance etc.
Understanding the data collected
We then encountered our first challenge and the problem I guess all the researchers who need to take surveys must be facing, the optimal number of questions to be asked so that we get the correct information from the 600 students who were filling the questionnaire at IIT Jodhpur. After a few trial and error rounds, we restrained ourselves to 2 section.
- The personal details about the person filling the questions, like age, hometown, caste, religion, branch, academic performance, and hobbies.
- To name 5-10 of his friends according to closeness. For each friend, there were additional five questions regarding who is more dominant, if he/she shares personal things with each other and how much time do they spend with each other.
After a month of hard work by the team, we finally received the data of all the 600 students, but the main and tedious task of any data analysis problem was yet to come, data cleaning. We were expecting that religion, caste, etc would be factors with not any levels, but then we found out that not all the students fill the questions with the same motive, (for eg. For religion one of the answers was, “I haven’t decided yet, but my parents follow Hinduism”). After a lot of pain, and omitting a few entries I was down to the task which we all had been waiting for, data analysis of the ‘clean’ data.
- Before Cleaning:
Total number of nodes: 584
Total number of edges: 1800 - After Cleaning:
Total Number of nodes: 549
Total Number of edges: 1262
Questions to be answered
- If both friends share the similar family background, are they friends?
- Are they friends if both of them speak the same language?
- Are they friend if both of them are from the same state?
- How is the inter-year relation at IIT Jodhpur?
- If both friends have the similar CPI, are they supposedly friends?
System Science batch 2017 contributed towards this project, under the guidance of Dr. Mainak Majumdar
OUTCOMES AND FINDINGS
- Degree Centrality is defined as the number of links incident upon a node (i.e., the number of ties that a node has)
For IIT Jodhpur network this was 5.311 - Degree distribution plot: Number of friends each student has.
- Closeness Centrality: The farness of a node x in a network such as ours, is defined as the sum of its distances to all other nodes, and its closeness is defined as the reciprocal of the farness.
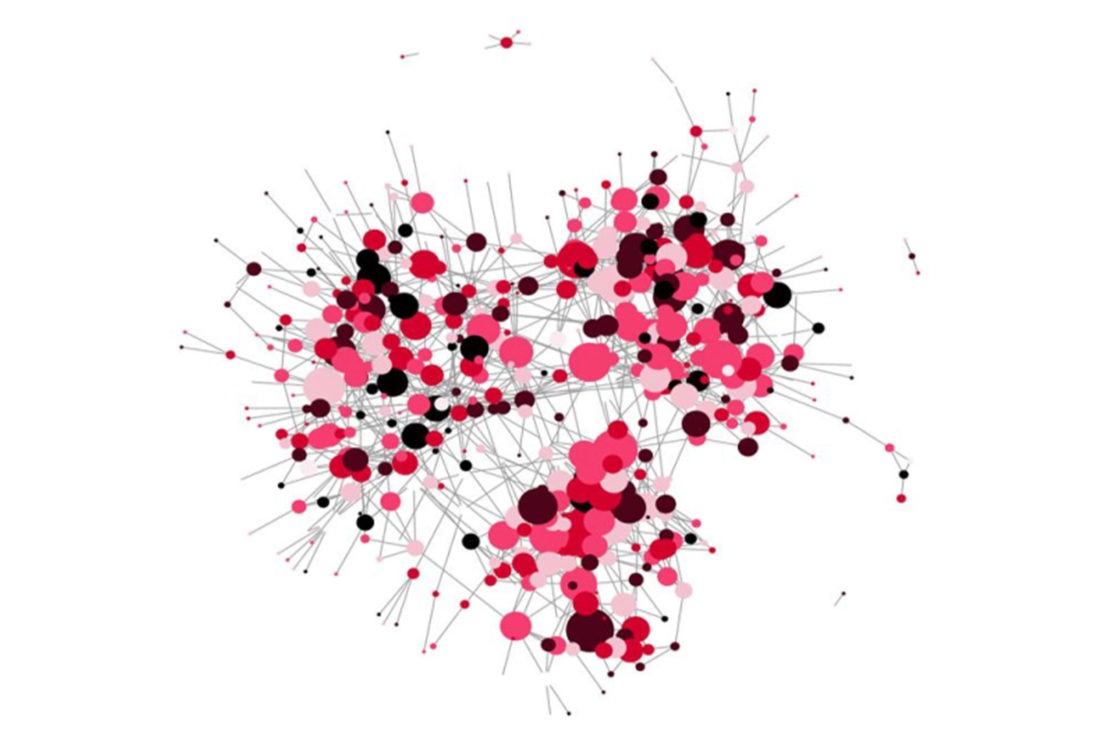
We can see that darker colours have lower closeness centrality because they are at extreme points. Nodes which do not belong to a cluster as well are having a low closeness centrality score. - Betweenness centrality quantifies the number of times a node acts as a bridge along the shortest path between two other nodes.Here we observed that betweenness of the nodes with high degree is high because there is more probability that the node acts as a bridge along the shortest path between two other nodes.
- Average Path length: It takes 5.38 links to reach from any person to any other person in the network. For the world, this is approximately 6
- Diameter: The shortest distance between the two most distant nodes in the network was 13
Now, let’s visualize the graphs to answer the questions because of which we started everything in the next tab.
INTERESTING VISUALIZATIONS
- Branch: There were no major clusters found because of the branch. Which means that the interdisciplinary relations are strong in IIT Jodhpur. When we are allocated rooms in our first year the institute make sure there are students of all branches in a room. Hence this makes sense.
- Category: Major clusters of General category make be observed, though there are a lot of inter-category friendship as well.
- Language: Students do make friends according to their language it seems. Students to studied in Hindi medium schools tend to stay together
- Academic performance: We can observe small clusters of light red colour and black colour implying that students tend to become friends with students having similar
- Relationship status: We can observe that students that are not in a romantic relationship tend to become friends with each other which are clear from the big black clusters. (Obvious, isn’t it?)
- Year of study: Large clusters can be seen among third years and fourth years.
We can’t find any clusters among first yearites because inter-yearear interaction.
IMPLEMENTATION IN R
R is an open sources language, hence the libraries available can do almost everything. Though the software Gephi is generally used for cluster analysis, it is very difficult to plot cluster graph to show various features like branch, year, etc. The library igraph is meant to do all these, so after a bit a deep dive into this library I started to implement the graphs needed which could be observed to find the conclusions.
The “trick” is to develop formal mathematical definitions that have known graph theoretic properties, and also capture important intuitive and theoretical aspects of cohesive subgroups.Katherine Faust